Phân phối chuẩn còn được gọi là phân phối Gaussian, trong tiếng Anh là Normal Distribution. UniTrain sẽ giúp bạn hiểu chính xác định nghĩa của phân phối chuẩn qua các khái niệm và ví dụ cụ thể dưới đây.
Khái niệm
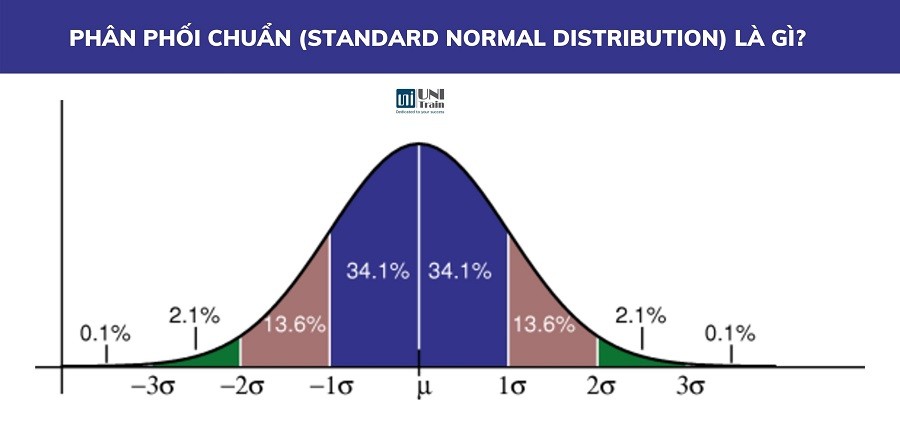
Phân phối chuẩn là loại phân phối phổ biến nhất hay được dùng giả định trong phân tích kĩ thuật thị trường chứng khoán và trong các loại phân tích thống kê khác. Phân phối chuẩn thông thường có hai tham số: giá trị trung bình và độ lệch chuẩn. Đối với phân phối chuẩn, 68% các quan sát nằm trong khoảng +/- độ lệch chuẩn của giá trị trung bình, 95% nằm trong +/- hai lần độ lệch chuẩn và 99,7% nằm trong + – ba lần độ lệch chuẩn.
Mô hình phân phối chuẩn được phát triển bởi Định luật giới hạn trung tâm. Lí thuyết này nói rằng các giá trị trung bình được tính toán từ các biến ngẫu nhiên độc lập và giống hệt nhau có phân phối gần với phân phối chuẩn, bất kể loại phân phối của mẫu mà các biến được lấy ra (miễn là nó có phương sai hữu hạn).
Phân phối chuẩn đôi khi bị nhầm lẫn với phân phối đối xứng. Phân phối đối xứng là một phân phối trong đó một đường phân chia sẽ tạo ra hai hình ảnh phản chiếu, nhưng dữ liệu thực tế có thể có hai bướu hoặc nhiều điểm nhô lên trên đường cong hình chuông của phân phối chuẩn.
Công thức
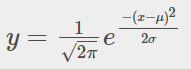
Với:
Trong đó:
Độ lệch chuẩn hay còn gọi là Standard Deviation. Là đại lượng dùng để phản ánh độ phân tán của các giá trị trong bộ dữ liệu. Thể hiện sự biến thiên của giá trị trong một thời điểm phản ánh xu thế của sự thay đổi.
Khi hai tập dữ liệu có cùng giá trị trung bình cộng, tập nào có độ lệch chuẩn lớn hơn là tập có dữ liệu biến thiên nhiều hơn. Trong trường hợp hai tập dữ liệu có giá trị trung bình cộng không bằng nhau, thì việc so sánh độ lệch chuẩn của chúng không có ý nghĩa.
Thông qua độ lệch chuẩn các nhà kinh tế, nhà quản lý có thể quan sát dự báo các thời kỳ biến động của nền kinh tế. Đối với các lĩnh vực khác cũng tương tự, độ lệch chuẩn luôn phân tích tính ổn định hoặc sự thay đổi cụ thể nào đó.
Ví dụ
Câu hỏi 1: Một khảo sát về thời gian di chuyển hàng ngày có kết quả như sau (tính theo phút):
| 26 | 33 | 65 | 28 | 34 | 55 | 25 | 44 | 50 | 36 | 26 | 37 | 43 | 62 | 35 | 38 | 45 | 32 | 28 | 34 |
Giá trị trung bình là 38.8 phút, độ lệch chuẩn là 11.4 phút. Đổi giá trị thành điểm z và vẽ đồ thị của phân phối chuẩn.
Lời giải:
Công thức cho điểm z chúng ta sử dụng là:
![]()
Với:
Để chuyển đổi giá trị 26:
Đây là ba giá trị chuyển đổi đầu tiên.
| Original Value | Calculation | Standard Score (z-score) |
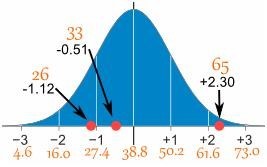
| 26 | (26-38.8) / 11.4 = | -1.12 |
| 33 | (33-38.8) / 11.4 = | -0.51 |
| 65 | (65-38.8) / 11.4 = | -2.30 |
| … | … | … |
Và đây là đồ thị biểu diễn:
Câu hỏi 2: Trọng lượng của một loại sản phẩm là đại lượng ngẫu nhiên có phân phối chuẩn với họng lượng trung bình μ = 5 kg và độ lệch tiêu chuẩn σ = 0,1. Tính tỷ lệ những sản phẩm có trọng lượng từ 4,9 kg đến 5,2 kg?
Lời giải: Gọi X là trọng lượng của loại sản phẩm này. Theo giả thiết thì X∼N(μ,σ2) với μ = 5 (kg); σ = 0,1
Tỷ lệ sản phẩm có trọng lượng từ 4,9 đến 5,2 kg chính là: P(4,9 ≤ X ≤ 5,2)
Áp dụng công thức (3.16) ta được:
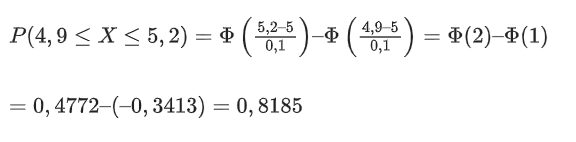
P(4,9≤X≤5,2)=Φ(5,2–50,1)–Φ(4,9–50,1)=Φ(2)–Φ(1)
=0,4772–(–0,3413)=0,8185
Tức tỷ lệ những sản phẩm có trọng lượng từ 4,9 đến 5,2 kg là 82%
Chú ý: Nếu dùng hàm NORMDIST để tính xác suất trên thì:
P(4,9 ≤ X ≤ 5,2)=NORMDIST(5.2,5,0.1,1) – NORMDIST(4.9,5,0.1,1) = 0,818595
UniTrain tổng hợp
Xem thêm
Combo 3 khóa học Data Analytics for Professionals
Độ lệch chuẩn (Standard Deviation) là gì? Ví dụ về Độ lệch chuẩn